Titanium CP/PF modelling - 2021 August

See the project overview for an outline. This page was last updated: September 2021

Following on from our preliminary low resolution crystal plasticity simulations, we then investigated ways to defined sub-grains within the deformed RVE.

Investigating methods of orientation-field clustering

A naive orientation-clustering approach

Conventional k-means clustering proceeds as follows:

1. Choose some trial cluster centroids
2. Assign each sample to its nearest cluster (according to, for example, a Euclidean distance metric)
3. For each centroid, compute the mean position of all the associated samples
4. Move the trial centroids to coincide with these sample-mean positions
5. Repeat steps 2 to 4 until the trial centroids no longer move (within some tolerance)

There are some issues with applying this method to the problem of sub-grain segmentation within an RVE. Firstly, we must be careful about choosing a suitable “distance” metric, since our samples are quaternions. Although these quaternions are represented as four-vectors, the Euclidean distance between two quaternion four-vectors does not seem particularly meaningful. Instead we should choose something that has meaning within the orientation domain, such as the angle between quaternions. Likewise, we must be careful about averaging orientation samples; a meaningful quaternion average can be calculated, which is distinct from an arithmetic mean of the quaternion vector components. However, even if we are careful to employ quaternion-specific maths in our implementation of k-means clustering, we have not yet encoded any spatial information into the algorithm. Thus, such an approach would result in disconnected (sub-)grains, which are composed of voxels that have been clustered together due to the similarity of their orientations without regard for the location of the voxels within the RVE.

We could perhaps implement a k-means orientation-clustering algorithm where the angle between quaternions is additionally weighted by their spatial separation. However, instead of this, we worked initially on a cost-function approach, as discussed below.

Minimise centroid positions according to the variance in orientations

Our initial approach was to:

1. Choose a set of centroid positions within the RVE
2. Assign each RVE voxel to its nearest centroid (thereby performing a discrete Voronoi tessellation)
3. Calculate an “average” quaternion for each Voronoi region
4. Calculate the quaternion “variance” for each Voronoi region (using the rotation angle between quaternions as the “distance” metric)
5. Wrap up steps 1. to 5. in a cost function that returns the sum of the region “variances”
6. Use the Nelder-Mead optimisation algorithm (as implemented in SciPy¹) with the above cost function to iterate on centroid positions

Unfortunately, using our current implementation, Step 2 (tessellation) is slow and memory intensive, which makes the optimisation very slow. Additionally, we must specify in advance how many clusters (i.e. centroid positions) we wish to use. Ideally, we would instead specify the “distance” (i.e. rotation angle) between the clusters.

We chose the Nelder-Mead algorithm since it is “gradient-free”, meaning the optimisation proceeds without the use of a gradient (i.e. a Jacobian or Hessian matrix). Other gradient-free optimisation algorithms also exist ², which we could try. These include the Powell algorithm ³ and the basin-hopping method ⁴.

We might investigate if using QHull as exposed in SciPy would be faster at performing discrete Voronoi tessellation than our implementation. If so, this could make the algorithm faster.

Existing methods in use to segment EBSD data

We should be able to use existing methods for grain segmentation within EBSD data. Surveying the literature, we found that the MatLab toolbox MTEX, in its calcGrains⁵ function, uses ^{6 7} one of two methods to segment (sub-)grains in EBSD data:

1. Markovian clustering ^{8 9}
2. Fast multiscale clustering
   • Implementation details in MTEX discussed in Ref. ¹⁰
   • Original algorithm discussed in Ref. ¹¹

The pipeline-based package Dream.3D also has a filter for segmenting grains, which we will investigate.

MTEX

The MTEX documentation gives some examples of loading in data from arbitrary text files¹². The first step was to generate from the deformed RVE a text file whose rows represent voxels and that contains columns with the following information:

• Phase (two phases in our data)
• Spatial coordinates: x, y, z
• Euler angles: Euler1, Euler2, Euler3

We have encounted some problems when trying to get MTEX to successfully load 3D data for grain segmentation; see the GitHub issue via Ref. ¹³.

Dream.3D

• The pipeline-based Dream.3D package can perform grain segmentation using the ScalarSegmentFeatures filter¹⁴.
• A previous discussion on the Dream.3D GitHub repository regarding importing results from crystal plasticity simulations into Dream.3D.
• Performing segmentation in Dream.3D requires an ImageGeometry, which is a uniform rectilinear grid. This means we cannot use the displacement information of each deformed voxel when doing this segmentation. However, I don’t think this matters.
• We have written a pipelines for performing the segmentation on a deformed RVE using a 128-cubed grid size. The deformed RVE and the resulting feature segmentation from the Dream3D pipeline is shown below. In this case we used a threshold misorientation angle of three degrees. I have yet to find a comprehensive description of the clustering algorithm that Dream3D uses for the segmentation, but it is reasonable to assume that our selected threshold means that neighbouring voxels that are misoriented by more than three degrees are considered to belong to distinct features (i.e. sub-grains).

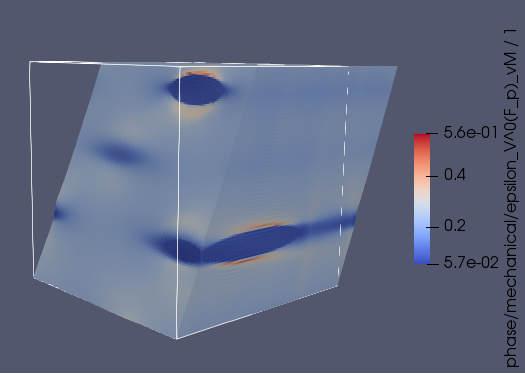
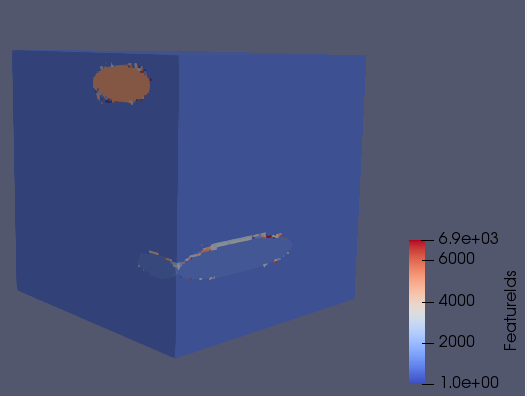
These preliminary results do not show significant formation of sub-grains, since the additional features are in very close proximity to the boundary of the $\alpha$ precipitates. We will continue to investigate this.

MatFlow integration

We have developed a MatFlow workflow (and associated task schemas/extension functionality) to perform the DAMASK simulations and grain segmentation using Dream.3D. More details will be provided as and when we concretise our analysis approach. However, an example task for generating the dual-phase RVE can be found here.

Quaternion component ordering conventions

During our development of the associated MatFlow workflow, we found that different software can employ different orderings of quaternion components; vector-scalar or, more commonly, scalar-vector:

• DAMASK: scalar-vector¹⁵
• MTEX: scalar-vector (I could not find an explicit statement, but from doing an Euler-to-quaternion conversion in MTEX, it seems so.)
• DefDAP: scalar-vector
• Dream3D: vector-scalar¹⁶

References