Titanium CP/PF modelling - 2021 September

See the project overview for an outline. This page was last updated: October 2021

Resource requirements

The crystal plasticity simulations must be performed with a sufficiently dense grid resolution. In particular, we must ensure:

1. smooth spatial variations of final stress/strain fields
2. sufficient modelling of the curved surfaces of the $\alpha$-phase particles
3. valid results when we later investigate the effects of the surface roughness of the $\alpha$-phase particles

To this end, we performed the same simple shear deformation on a set of volume elements with grid sizes ranging from (32 $\times$ 32 $\times$ 32) to (256 $\times$ 256 $\times$ 256).

Lower- and higher-resolution RVEs

The simulation durations and memory consumptions are plotted below, where grid sizes 32 and 64 where run using eight CPU cores, grid sizes 128 and 192 were run using 16 cores, and grid size 256 was run using 32 cores.

Alignment issues

We ran the fast multiscale clustering (FMC) routine in MTEX on the $y=0$ slice of the deformed RVE, using $C_\text{Maha} = 2.5$. The figure below shows how the clustering process splits up the image into “grains”. However, given that we would not expect much rotation of the hexagonal $\alpha$-phase, the inverse-pole-figure (IPF) colouring in the below figure is odd, since it indicates that the ellipsoidal $\alpha$-phase particle has $[\bar{1} 1 0 0]$ (blue) direction in the $y$-direction (out of the page). Instead, we would expect to see an $a$-direction $[\bar{1}2\bar{1}0]$ (see July’s blog post for details of the RVE construction).

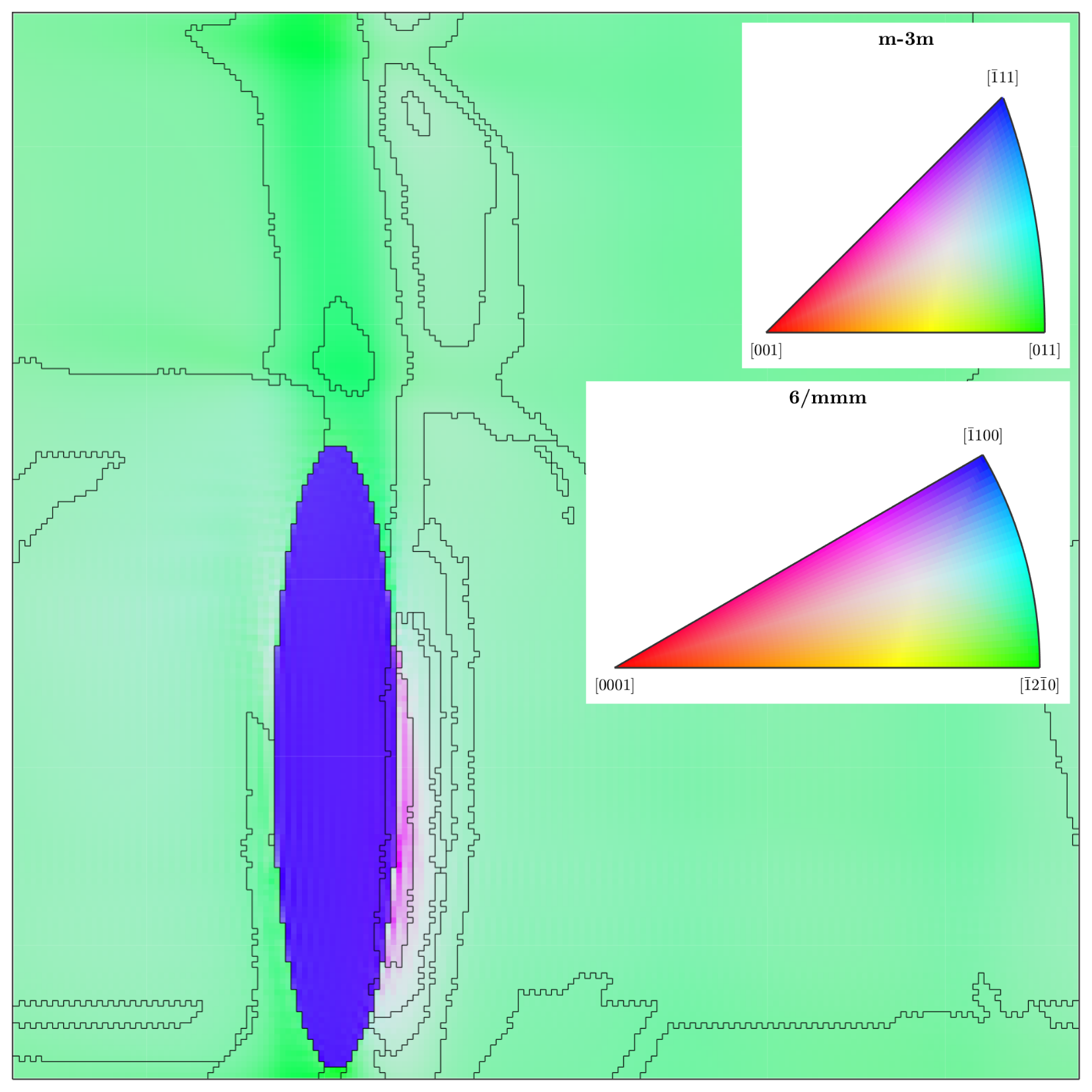2D FMC grain segmentation of the $y=0$ slice, with incorrect alignment of the hexagonal unit cell

In fact, this is incorrect, and arises from the different hexagonal unit cell alignments used by DAMASK and MTEX. To fix this issue, we must specify in MTEX the same alignment system that DAMASK uses, which is to align the $x$-axis with the $a$-direction of the hexagonal unit cell. This is done when defining the crystalSymmetry object: crystalSymmetry('hexagonal', 'mineral', 'Ti (alpha)', 'X||a') — note the X||a.

Comparison of clustering parameter $C_\text{Maha}$

After correcting the alignment issue above, we ran the clustering for a range of different values of $C_\text{Maha}$, which controls how large the clusters will be. This is shown in the below figure.

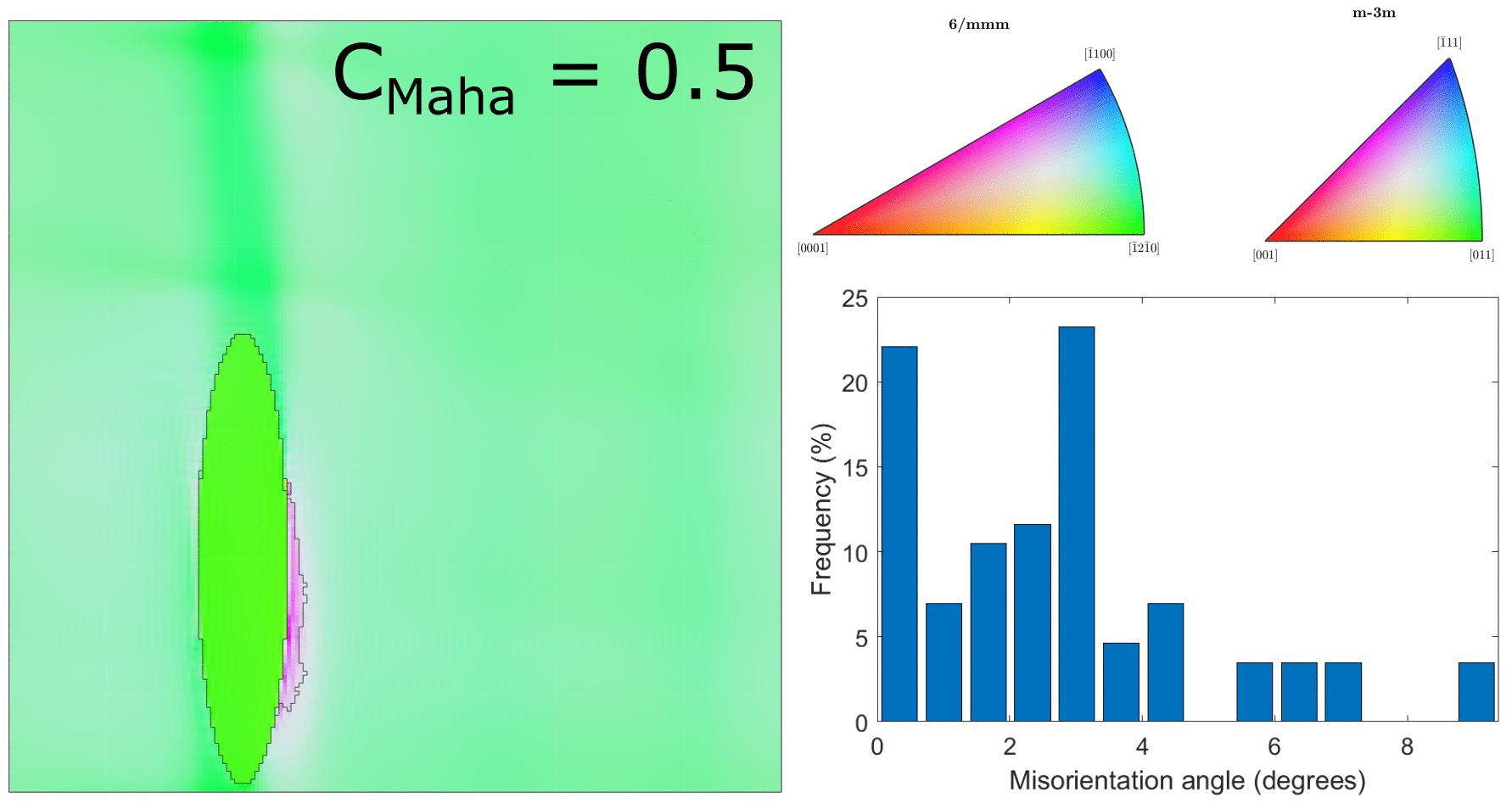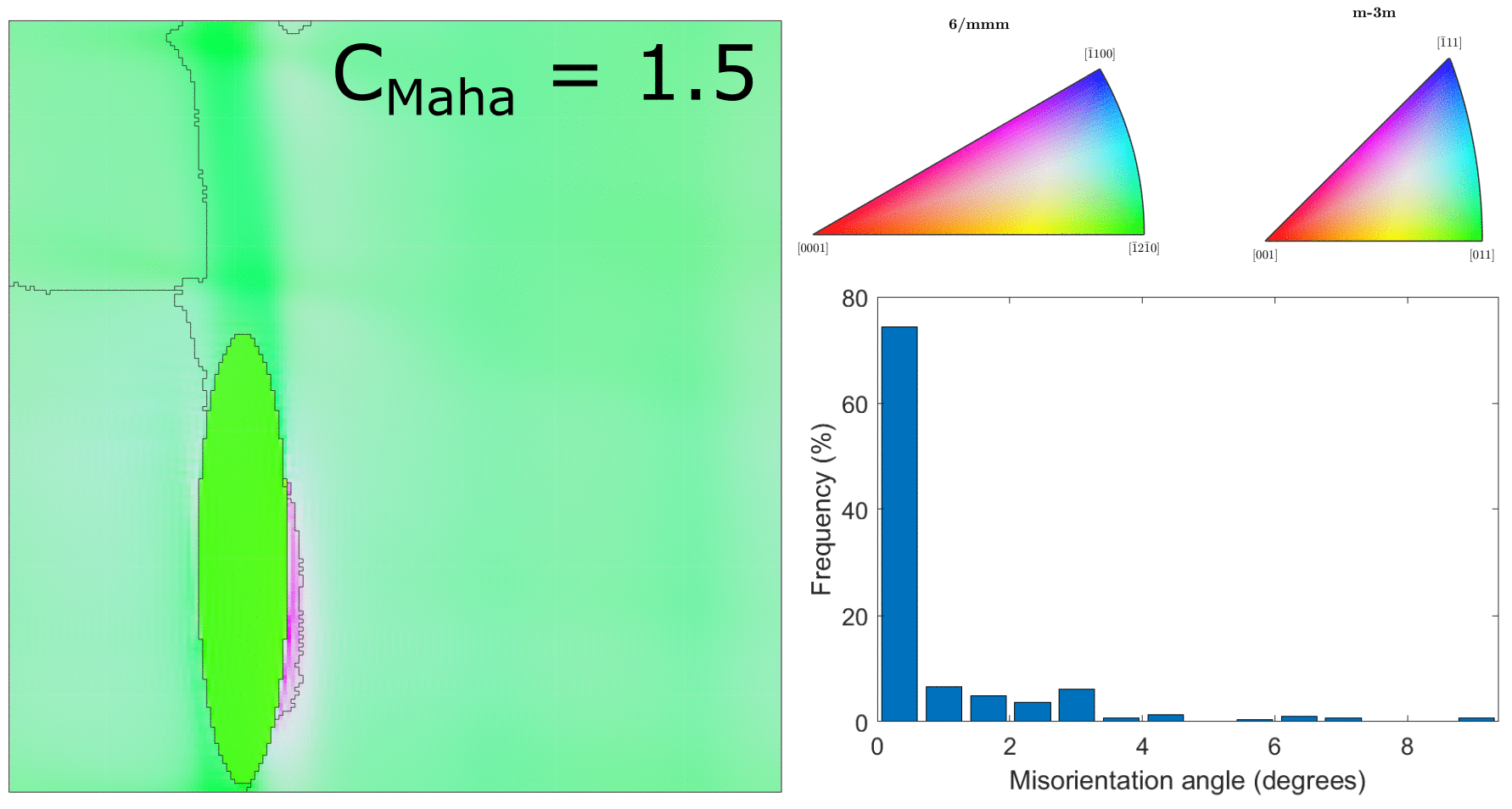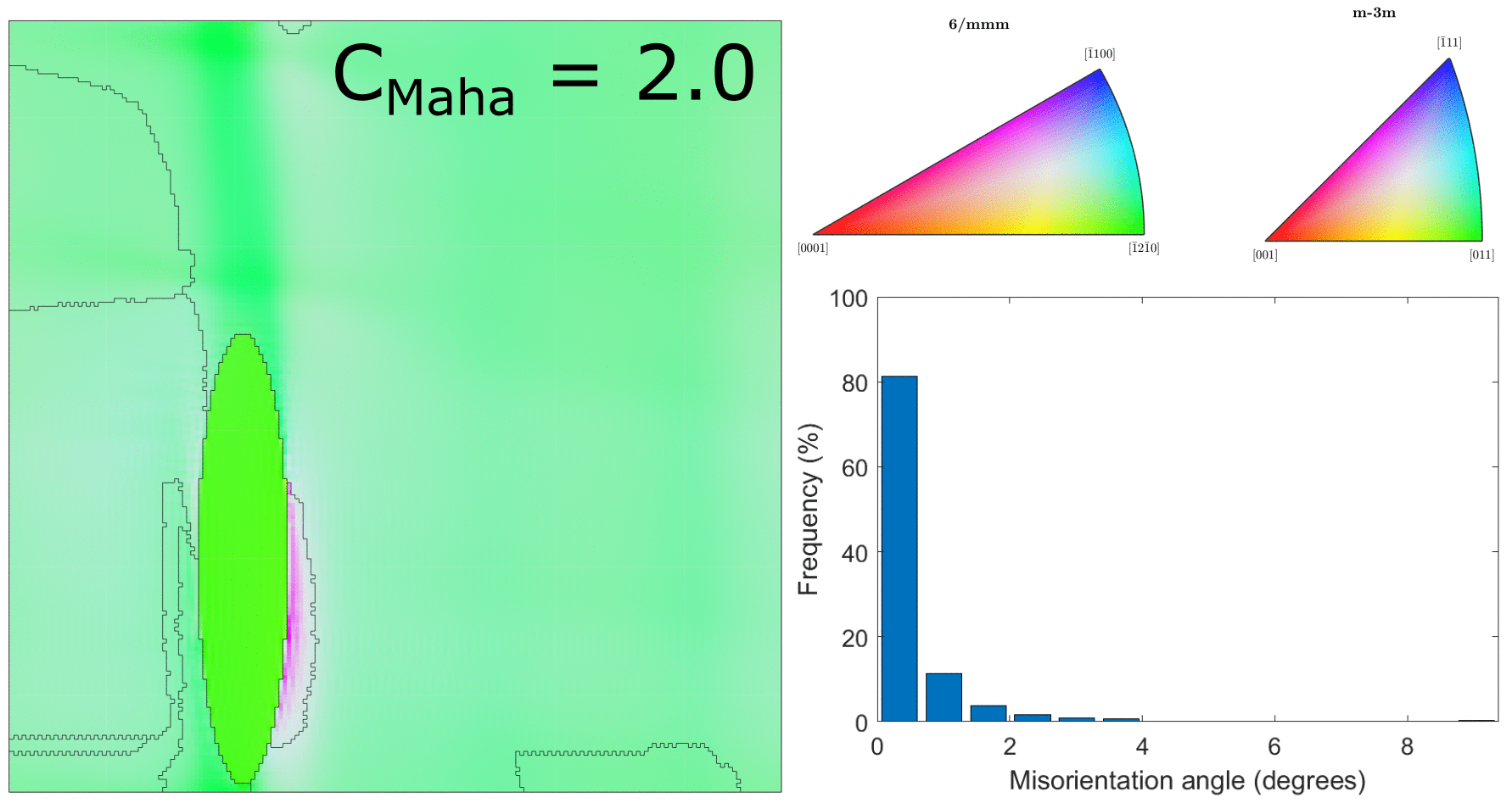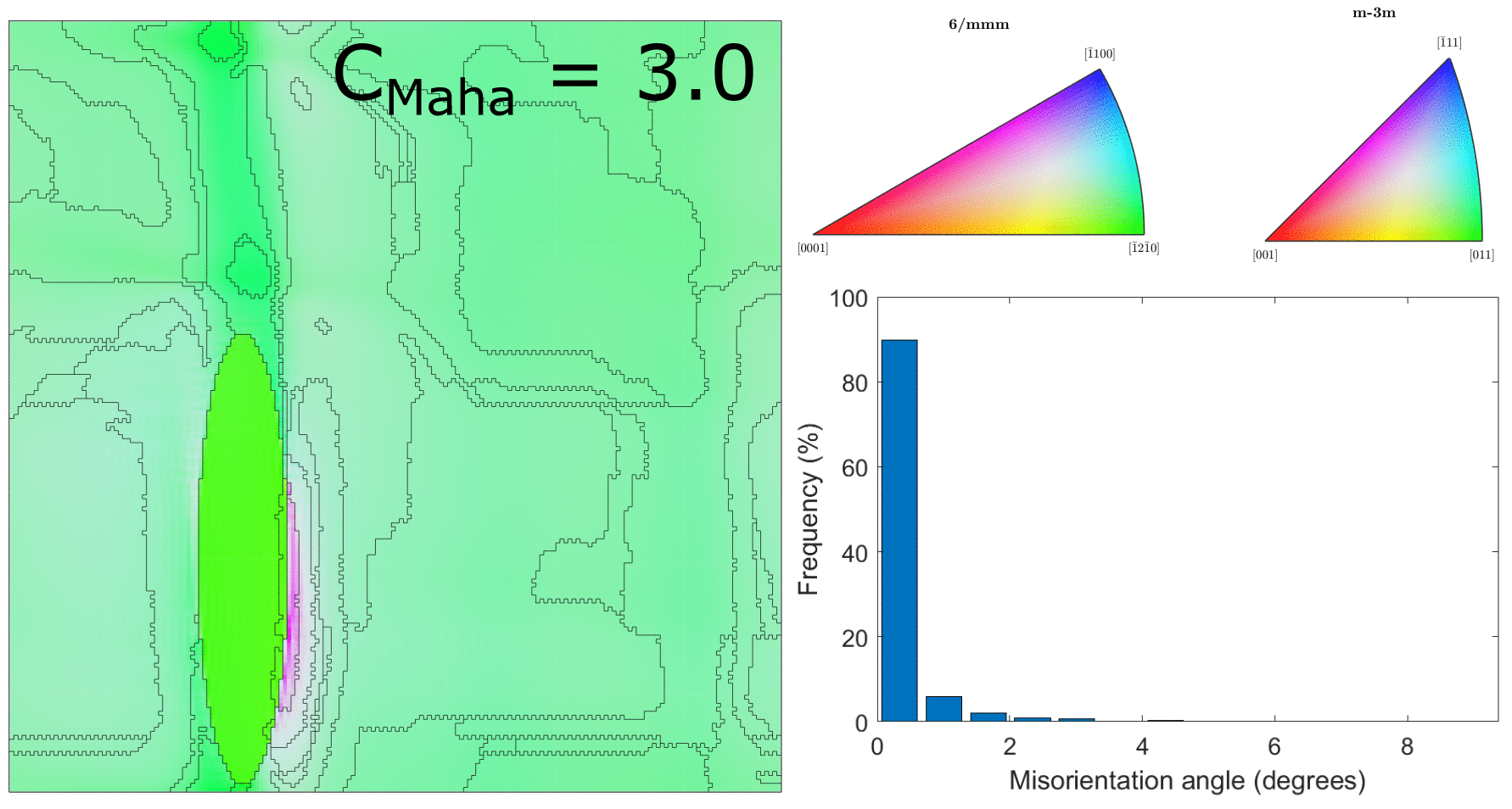Clustering for values of $C_\text{Maha} = \{0.5, 1.0, 1.5, 2.0, 2.5, 3.0\}$ (with correct hexagonal unit cell alignment!)

Accounting for periodicity

Since the RVE that was simulated was periodic, we need to consider this when performing the clustering. To do this, we tiled the 2D slice into a $3 \times 3$ grid of 2D slices, and performed the clustering on this new, larger slice instead. Cropping the resulting image of the clustered grains back to the size of the original slice, we can see some subtle differences in the result of the clustering due to the periodicity, as portrayed in the figure below.

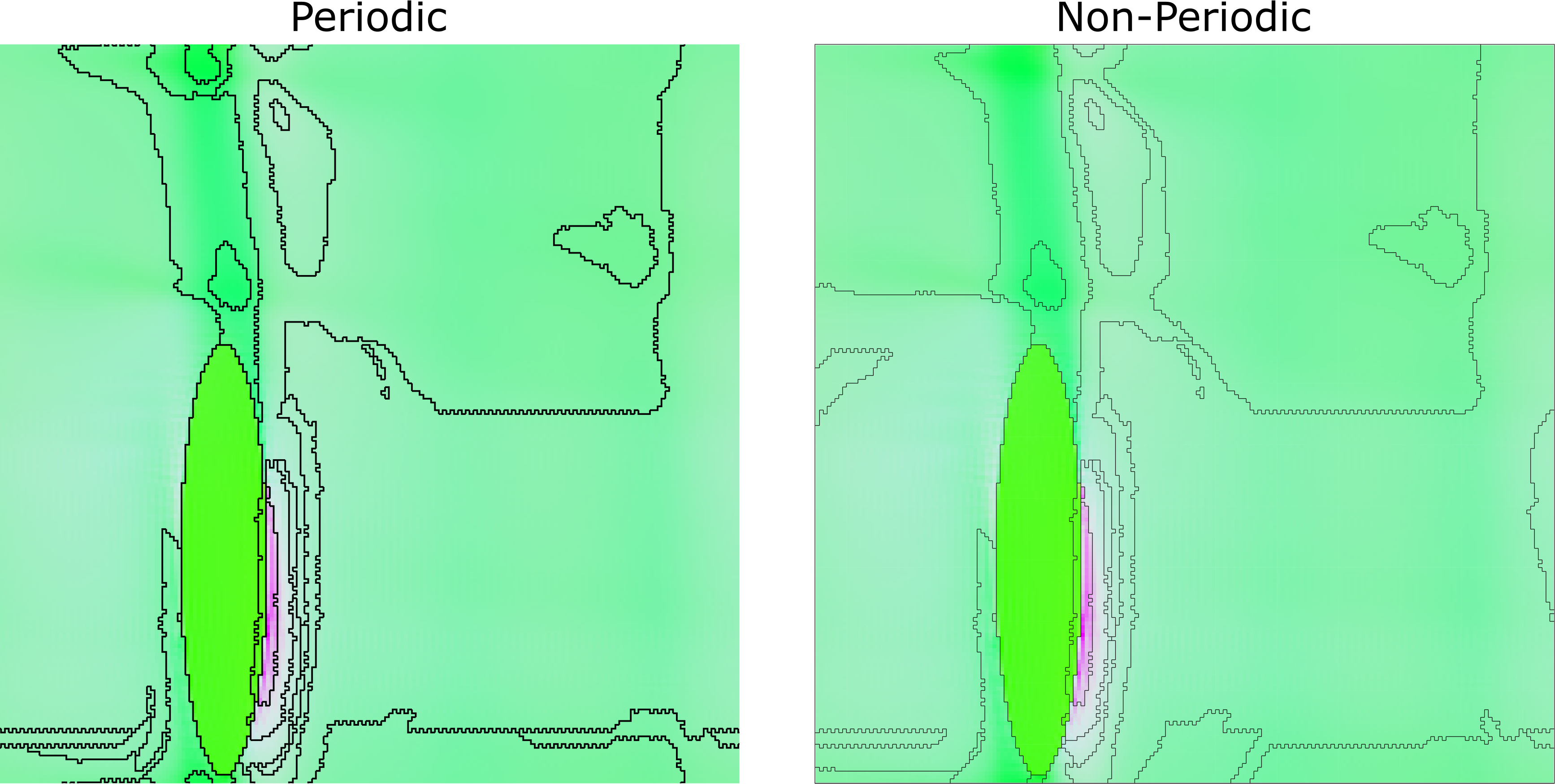We must consider periodicity in the grain clustering. Doing so has an effect on the morphology of the clustered grains. (Example using $C_\text{Maha}=2.5$ and no smoothing.)